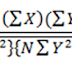Menghitung Cepat

Cobalah hitung:
51² = …
52² = …
53² = …
Dan seterusnya sampai
59² = …
Tentu kita dapat menghitungnya dengan cara seperti biasa. Kita juga dapat menyelesaikannya dengan kalkulator. Tetapi apa kreatifnya? Apa asyiknya? Inilah cara asyiknya!

·         54² = 2916

29 kita peroleh dari 25 + 4

16 kita peroleh dari 4²

·         562 = 3136

31 kita peroleh dari 25 + 6

36 kita peroleh dari 62

·         572 = 3249

32 kita peroleh dari 25 + 7

49 kita peroleh dari 7²

Sets

Sets

6.1.             Understanding Sets

The concept of set was first proposed by a German mathematician named Georg Cantor who lived from 1845-1918.

A set is a collection of object which can be clearly defined.

v  Collections or groups  considered as sets

Example :

1. A group of alphabet,
2. A group of even number,
3. A group of students in your class who wear black shoes, etc.

v  Collections or groups not considered as sets

Example :

1. A group of beautiful girls in library,
2. A group of naughty kids in the yard,
3. A group of students who are smart in your class, etc.

v  Symbol of a Set

A set may be expressed using braces and is usually denoted by a capital letter such as A, B, C, D, and so on until Z. If two or more different sets are involved, then the names of those sets must be different from each other.

Example :

A = a group of cute children

B = a group of animals

6.2.             Membership in a Set

Objects which are included in a set are called members or elements of that set.

We use symbol Î, to show that object is a member of a set

We use symbol Ï, to show that object is not a member of a set

Every member is mentioned only once.

Example :

There are 5 bananas, 3 apples, 2 mangoes, and 4 pineapples. We can write

B = {banana, apple, mango, pineapple}

v  Number of Members of a Set

Denoted by n.

Example :

A = {1, 2, 3, 4, 5 , 6} à n(A) = 6

v  Sets of Numbers

The set of all integers, B = {…, -2, -1, 0, 1, 2, …}

The set of all natural numbers, A = {1, 2, …}

The set of all counting numbers, C = {1, 0, 1, 2, …}

Etc.

6.3.             Describing a Set

a.       By Words

b.      Using Set-builder Notation

c.       By Extension

Example :

A is the set of the first five counting numbers.

§  By Words

A = {the first five counting numbers}.

§  Using Set-builder Notation

A = {x ê0 ≤ x ≤ 4, x is a counting numbers}.

§  By Extension

A = {0,1,2,3,4}.

6.4.             Empty Sets

An empty set is a set which has no member.

Denoted by { } or Ø.

Examples :

A set of natural numbers between 1 and 2,

A set of all months whose name starts with Z, etc.

6.5.             Universal Sets

A universal set is a set which contains all members of the set under consideration.

It’s also called a universe.

Denoted by S.

Example :

A = {all students in faculty of mathematics and science}

B = {all students in faculty of economic}

Then,

S = {all students in Semarang State University}

6.6.             Venn Diagram

The rules for building a Venn Diagram :

•          Represented by a rectangle with a letter S on the upper left corner

•          Every member of universal set is represented by a dot

•          Every set contained in the universal set is represented by a simple closed curve

•          To represent a set which has a very large number of members in the Venn diagram, dots are not used.

Example :

S = {1, 2, …, 10}

A = {1, 3, 5, 7, 9}

B = {1, 2, 3, 4, 5]

 

6.7.             Subsets

A subset B, if each member of set A is also member of set B.

Denoted by A Ì B.

Every set is a subset of itself.

A Ì B = “A is contained of B”

B É A = “B contains A”.

v  Find The Number of All Possible Subsets of a Set The number of subsets Using The Pattern in Pascal’s Triangle

The Number of All Possible Subsets of a Set = 2ⁿ

Example :

K = {1, 2, 3, 4, 5}

n(K)= 5
The number of all possible subsets of K = 2⁵ = 32.

6.8.             Intersection of Sets

The intersection of sets A and B is a set whose members are the members of both the sets A and B simultaneously, be defined as A Ç B.

By using set-builder notation we can defined as:

A Ç B  = {x │ xÎA and xÎB}

Example :

A = {Devi, Ari, Andre, Indah}

B = {Jatu, Devi, Ari}

A Ç B = {Devi, Ari}

6.9.             Union of Sets

The union of the sets A and B is a set whose members are the members of A only, the members of B only, and the common members of A and B.

 

    A È B = A + B – A Ç B

or by using set-builder notation we can defined as:

A È B  = {x │ xÎA or xÎB}

Example :

A = {Devi, Ari, Andre, Indah}

B = {Jatu, Devi, Ari}

A È B = {Devi, Ari, Andre, Indah, Jatu}

6.10.         Difference of Sets

A – B is the set of all members of A which are not the members of B.

May be defined as:

A – B = {x │ xÎA or xÏB}

Example :

A = {Devi, Ari, Andre, Indah}

B = {Jatu, Devi, Ari}

A – B = {Andre, Indah}

6.11.         Complement of Sets

The complement of set A is the set whose members are those members of S which are not members of A.

A’ = {x │ xÏA and xÎS }

Example :

S = {1, 2, 3, …, 10}

A = {2, 4, 6, 8, 10]

Then, 

A’ = {1, 3, 5, 7, 9}

Exercise :

1.       Give 5 sentences of group which serve as sets, and name four members of each group!

2.       Let :

P = {1, 2, 3, 4, 5, 6}

Q = {2, 4, 6}

Determine the relationship between the set P and  the set Q!

3.       Tell whether each of the following sentences id true or false!

a.       5 Î {1, 3, 5, 7}

b.      6 Î {even numbers}

c.       a Î {capital letters}

d.      Î {1, 3, 5, 7}

4.       P = {odd counting numbers which are less than 16 and evenly divisible by 3}.

Describe set P by :

a.       Set-builder notation

b.      extension